|
What we have done so far
- First week:
- Geometry of linear equations.
- Length (norm, magnitude) of a vector with n components. Dot product of two vectors.
- Elimination method. Cost of this algorithm.
- Singular and non-singular systems.
- Matrix multiplication.
- Use of blocks in multiplication.
- Second week:
- Elementary matrices.
- LU decomposition (with no changes of rows).
- Use of LU in solving linear equations.
- Permutation matrices.
- PA=LU (with change of rows).
- Sign of a permutation.
- Uniqueness of LDU decomposition.
- Multiplying by a diagonal matrix from left (or right).
- Transpose of a matrix.
- Symmetric matrix.
- (AB)T=BTAT.
- Third week:
- If LDU is symmetric, then L=UT.
- Inverse of a matrix.
- Right inverse=left inverse (if both of them exist).
- Square matrix+ left inverse ----> invertible.
- P-1=PT if P is a permutation martix.
- A-1=AT if A is an orthogonal matrix.
- Eij(c)-1= Eij(-c).
- (AB)-1=B-1A-1 if both A and B are invertible.
- If AB and B are invertible, so is A.
- How to find inverse of a matrix. (only in one of the classes)
- If A is invertible, Ax=0 (column vectors) and yA=0 (row vectors) have unique vector solutions, x=0 and y=0, respectively.
- Necessary and sufficient condition for an upper-triangular matrix to be invertible. (Diagonal entries should be non-zero.)
- A is invertible if and only if AT is invertible. Moreover if they are invertible, (AT)-1=(A-1)T.
- PA=LU; A is invertible if and ony if all the diagonal entries of U are non-zero.
- If A is not invertible, then there is a non-zero vector x such that Ax=0.
- Definition of a vector space.
- Examples of vector spaces from "linear" differential equations, e.g.
{f:[0,1] &rarr R | f is differentiable, f''(x)-f'(x)-f(x)=0}.
- Examples of vector spaces from "linear" recursive sequences, e.g.
| {{an} |
∞ n=1 |
|an's real numbers & an+2=an+1+an for any positive integer n}. |
- Linear transformation TA(x)=Ax associated with a given matrix A.
- Image of TA=the column space of A=linear combination of columns of A.
- Null space (or kernel) of A.
- Echelon form of A.
- Using elemination process to describe the column space and the null space of A.
- How to describe "preimage of a vector b under TA", i.e. solutions of Ax=b.
- Forth Week:
- Reduced row echelon form of a matrix.
- How to describe solutions of Ax=b, using rref(A).
- Ax=b has either 0, 1, or infinitely many solutions (revisited).
- If xp is a solution of Ax=b, then any soltuion of this system of linear equations is of the form xp+xn, where xn is a vector in Null(A) the null space of A.
- If A is n by m and m>n, then Null(A) is non-zero, i.e. if the number of variables is more than the number of equations in Ax=0, then there is a non-zero solution.
- Let A be square matrix; then A is invertible if and only if Null(A)={0}.
- Rank(A)= number of leading 1's in the rref(A).
- Linearly independent vectors.
- v1, v2, ... , vn are linearly independent if and only if the null space of A=[v1 ... vn] is zero.
- Columns of an invertible matrix are linearly independent.
- Rows of an invertible matrix are linearly independent.
- Spanning sets.
- Columns of a matrix span the column space.
- Define a basis.
- dim (Rn)=n.
- How to find a basis of the null space and the column space.
- Null(A)=Null(rref(A)).
- dim (column space of A)=rank(A).
- Fifth week:
- row space of A=row space of rref(A).
- dim (row space of A)= rank(A).
- rank(A)=rank(AT).
- dim (left null space of A)= #rows-rank(A).
- dim (Null space of A)= #columns-rank(A).
- Let T:Rn &rarr Rm be a linear transformation; Then
dim(Rn)=dim(ker(T))+dim(Im(T)).
- If A has a right-inverse, then the left-null space of A is zero.
- If A has a left-inverse, then the null space of A is zero.
- Left-null space of A is zero if and only if rank(A)= #rows.
- Null space of A is zero if and only if rank(A)= #columns.
- If rank(A)= #rows, then A has a right-inverse.
- The following statements are equivalent:
- A has a left inverse.
- N(A)={0}.
- rank(A)=# columns.
- If Ax=b has a solution, it is unique.
- The row space = R# columns.
- For any b, xTA=bT has a solution.
- AT has a right inverse.
- Any finite dimensional (real) vector space V can identified with Rdim V.
- Let B={v1,...,vn} be a basis of V. For any v in V, let
[v]B=[c1 ... cn]T,
where v=c1 v1+...+cnvn. Then [.]B:V &rarr Rn is a 1-1 and surjective linear map.
- Let B1={v1,...,vn} and B2={w1,...,wn} be two basis of V. Then the following diagram is commutative:
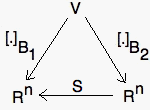 where S=[[w1]B1...[wn]B1], i.e. [v]B1=S [v]B2.
where S=[[w1]B1...[wn]B1], i.e. [v]B1=S [v]B2.
- Let T be a linear transformation from V to W, B={v1,...,vn} a basis of V, and B'={w1,...,wm} a basis of W. Then the following diagram is commutative:
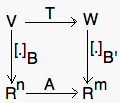 where A=[[T(v1)]B'...[T(vn)]B'], i.e. [T(v)]B'=A [v]B.
where A=[[T(v1)]B'...[T(vn)]B'], i.e. [T(v)]B'=A [v]B.
- Sixth week:
- The following diagram is commutative:
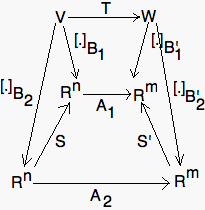 where S, S', A1, and A2 are similar as above. It is the same as saying that
A2=S'-1 A1 S.
where S, S', A1, and A2 are similar as above. It is the same as saying that
A2=S'-1 A1 S.
- Let T be a linear transformation from V to V. Let B1 and B2 be two basis of V. In the above setting, let W=V, B'1=B1, and B'2=B2; then
S'=S and A2=S-1 A1 S.
- We say that A is similar to B if A=S-1 B S, for some S.
- Description of matrix of rotation in the standard basis.
- Description of matrix of projection onto a line and more generally onto a direction in Rn in the standard basis.
Proja(v)=(a.v/a.a)a=(1/aTa) a (aTv)=(1/aTa) (a aT) v.
So in the standard basis, its matrix is (1/aTa) (a aT), which is a symmetric matrix.
- Remark: since we used the dot product for the projection, we are writing v in the standard basis (or orthonormal basis which we will learn later).
- Description of matrix of reflection about a line which passes through the origin.
RefL(v)+v=2 ProjL(v),
therefore
RefL(v)=2 ProjL(v)-v,
and we get what we wanted.
- Changing the standard basis and showing that the projection matrix is similar to
and the reflection matrix is similar to
- Othogonal complement of a subspace.
- Let V be a subspace of Rn; (V ⊥) ⊥=V.
- Let V be a subspace of Rn; then Rn=V ⊕ V ⊥, i.e. any vector b in Rn can be written as a sum of a vector v in V and v ⊥ in V ⊥ , in a unique way.
- If b=v+v ⊥ , where v is in V and v ⊥ is in V ⊥ , then ProjV(b)=v and ProjV ⊥ (b)=v ⊥ .
- ProjV+ProjV ⊥ =idRn.
- Let V be a subspace of Rn, x and y two vectors in Rn; then x=ProjV(y) if and only if
- x is in V,
- y-x is in V ⊥ .
- C(A)⊥=N(AT). (Similarly, C(AT)=N(A)⊥.)
- Let A be an n by m real matrix, TA the associated linear transformation from Rm to Rn; then restriction of TA is an isomorphism between the row space C(AT) and the column space C(A), i.e. it is a linear map whose kernel is zero and whose range (image) is the co-domain.
- Getting the best possible answer to an inconsistent system of linear equations Ax=b.
- Normal equation associated with a least-square problem: ATA x=ATb.
- N(ATA)=N(A).
- C(ATA)=C(AT).
- If columns of A are linearly independent, then
- ||Ax-b|| is minimize at
x= (ATA)-1AT b.
- Matrix P of ProjC(A) the orthogonal projection onto the column space of A in the standard basis is equal to
A(ATA)-1AT
- Seventh week:
- Linear least square method.
- The same method works for the other kind of expected functions, i.e. as long as we expect that our output is a linear combination of a finite set of given functions. For example, if we expect to get a polynomial of degree n, then A=[aij] such that aij=tij-1.
- If P2=P and PT=P, then it represents an orthogonal projection onto C(P).
- If P is projection onto a subspace V, then C(P)=V.
- We say that a map T:Rn→ Rm preserves the Euclidean structure if
- ||T(x)-T(y)||=||x-y|| for any x and y.
- Angle between the segments T(x)T(y) and T(y)T(z)= angle between the segments xy and yz.
- If T:Rn→ Rm is a linear map which preserves the Euclidean structure and Q is the matrix associated with T in the standard basis, then
- Columns of Q have length 1.
- Columns of Q are pairwise orhtogonal to each other.
- If Q is an m by n matrix such that
- Columns of Q have length 1 and
- Columns of Q are pairwise orhtogonal to each other,
then
- QTQ=In,
- (Qx).(Qy)=x.y,
- ||Qx||=||x||,
- ∠(Qx,Qy)=∠(x,y).
- Let T:Rn→Rm be a linear transformation. The following statements are equivalent:
- ||T(x)||=||x|| for any x.
- T(x).T(y)=x.y for any x and y.
- ||T(x)||=||x|| and ∠(T(x),T(y))=∠(x,y).
- Definition of orthonormal, orthonomal basis and orthogonal matrices.
- QTQ=In if and only if the columns of Q are orthonormal.
- If Q is a square matrix and its columns are orhtonormal, then its rows are also orthonormal.
- If qi's are non-zero and pairwise orhtogonal to each other, and
b=c1q1+...+cnqn,
then
ci=(qi.b)/(qi.qi).
- If ai's are linear independent, how we can find the projection of a given vector onto the span of ai's. (Let A be a matrix whose columns are ai's and then use A(ATA)-1AT.)
- We can also find an orthonormal basis for the of span of ai's and then use dot product.
- If the columns of Q are orthonormal, then the matrix of projection onto the C(Q) in the standard basis is QQT.
- Gram-Schmidt process, i.e. let ai be linearly independent vectors.
| bj:=aj-&Sigma |
j-1
i=1 |
(qi.aj)qi
|
- qj=bj/||bj||,
then qi's are an orthonomal basis of the span of ai's.
- How to use Gram-Schmidt to find an orthonormal basis of span of given vectors.
- If the columns of A are linearly independent, then A=QR, where Q has orthonormal columns and R is an upper-triangular matrix. (A is not necessarily a square matrix.)
- If columns of A are ai's, and qi's are the outcomes of the Gram-Schmidt process, then the for i at most j, the ij entry of R is qi.aj.
- Eighth week:
- What a ring is.
- det:Mn(R) → R s.t.
- det(In)=1.
- Exchange of rows changes the sign.
- Linear w.r.t. the first row.
- Linear w.r.t. any row.
- Equal rows ⇒ det=0.
- (resticted) Row operations does not change.
- Zero row ⇒ det=0.
- A triangular ⇒ det(A)=product of its diagonal entries.
- A is singular iff det(A)=0.
- PA=LU ⇒ det(A)=sgn(P) product of diagonal entries of U.
- Product rule: det(AB)=det(A)det(B).
- det(A)=det(B) if A and B are similar.
- det(T) is well-defined when T:V→ V is a linear transformation.
- Transpose rule: det(A)=det(AT).
- "Big formula"
| det(A)=Σ |
s in Sn |
sgn(s) Π |
n
i=1 |
ais(i). |
-
| det |
|
| |
A
0 |
|
B
C |
|
| |
= det(A) det(C). |
- Aij: (n-1) by (n-1) matrix after deleting the i th row and the j th column of A.
- For any i between 1 and n,
| det(A)=Σ |
n
j=1 |
(-1)(i+j) det(Aij) aij |
- For any i and k between 1 and n, if k is not equal to i,
| 0=Σ |
n
j=1 |
(-1)(i+j) det(Aij) akj |
- The ij entry of the adjoint of A is (-1)(j+i) det(Aji).
- A adj(A)=det(A) In.
- Using transpose: adj(A) A=det(A) In.
- If A is invertible, A-1=adj(A)/det(A).
|
