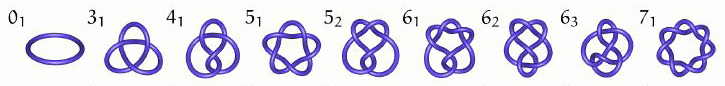
My office hours are Wednesday and Friday 11-12 (right after class) in AP&M 7210.
Homeworks will normally be due on the Monday following the section at 4pm. There's a dropbox in the AP&M basement. Midterm will be in class on Friday Feb 8. Final is on Friday March 22nd at 8am in ****.
Grading will be 30% homework, 20% midterm, 50% final.
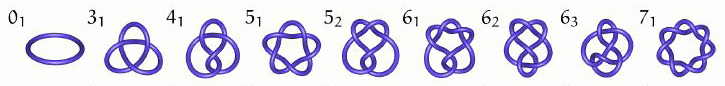
To prove this we need to apply some algebraic topology (e.g. the fundamental group of the complement of the knot in space), geometric topology (e.g. looking at surfaces associated to the knot - we will spend some time on the topological classification of surfaces in its own right), combinatorial topology (e.g. counting 3-colourings of a diagram, or the famous Jones polynomial) or other cleverness. The study of knots is both a testbed in which to apply the abstract theory of topology, and a source of new problems and methods. Plus of course it's fun! (Challenge: make a trefoil as above, and then make one where all the overcrossings go under and vice versa. Are they the same?)
C. Adams, The Knot Book (1994, W. H. Freeman) This book is a survey of knot theory. It isn't a typical textbook - it is not very detailed mathematically, since it's actually aimed at clever high-school students! But it does attempt to give the flavour of some really quite advanced topics, including current research and open problems!
M.
Armstrong, Basic Topology (1983, Springer-Verlag).
This is a nice undergrad-level book which teaches point-set topology
and the foundations of algebraic topology. It's not directly
relevant to the course, but if you are interested in point-set
topology, this is probably the best place to look.
N. Gilbert and T.Porter, Knots and Surfaces (1994, OUP) An undergrad-level book, which as I remember contains some basic point-set topology too. Its focus is extremely algebraic, however - it goes into group-theoretic aspects in a lot of detail.
A. Sossinsky, Knots, (2004, Harvard). This is a translation of a French edition, "Noeuds". It is quite idiosyncratic, and has a lot of typos and mistakes, so I don't much recommend it. However, you simply must check out the awesome picture of a particular type of eel which knots itself in order to stay slippery!W.
B. R. Lickorish, An
Introduction to Knot Theory (1997, Springer GTM) The
"new testament" of knot theory, a graduate-level textbook dealing
especially with post-Jones-polynomial knot theory. It's by my PhD
advisor - you might enjoy his dry wit!
There
are lots of knot theory resources on the web these days - these are
the main ones that spring to mind. You'll learn a lot just by
surfing these sites, and they also provide tables of calculations of
pretty much every knot invariant you can think of, some software for
drawing and calculating with knots, and beautiful images.
The
Knot Atlas (wiki)
The KnotPlot Site
Traditionally, we teach the more geometric, visual side of the subject after teaching all the basic tools. This is not unreasonable, but it does take a long time to do properly, and is quite hard to motivate because it turns history on its head. After all, people have been using and thinking about knots for thousands of years, but the definition of a topological space is only a hundred years old.
Fortunately it isn't necessary to work this way
round. With a little care we can do quite a lot of knot theory without
needing to talk about the foundational aspects of topology.
The follow on Math 191 course will be more of a "traditional" algebraic topology course.
One of the common problems faced by students in topology is deciding how much detail to write in proofs; the subject spans a great range, from the most pedantic and precise point-set arguments, to visual arguments which can seem like ``hand-waving''. I hope that the course will help you in general to appreciate and produce ``good mathematics'' at whatever level is appropriate.
You may find the homework questions a bit strange to start with... DON'T PANIC! Here are a few comments.
1. They are not like calculus
problems, where you just manipulate formulae and write "equals, equals, equals" down the
left-hand side of the page! The idea is generally to prove
things.
2. A proof will often amount to just presenting a logical argument or explanation in English. Don't be afraid to write plenty of words - just make sure that they are clear meaningful words, and not waffle! You may feel that a verbal argument isn't really mathematical, but this is not true: maths is about the precise communication of precise ideas, and they don't always need to contain formulae and funny symbols.
3. Please try to write coherently!
One helpful tip is to keep a particular reader in mind: imagine that
you are trying to convince a fellow member of the class that something
is true, and that they will not necessarily `know what you mean' if
you write unclear, vague and confusing things, and will argue with you
if there are gaps in what you say.
4. In a high-level subject like
topology, you often have to use a bit of judgment to decide how much
detail to put into your argument; this comes mostly with experience.
If, for example, you find you need to appeal to some `obvious'
fact,first ask yourself whether it really is obvious! Are you
confident that you could prove it if challenged? If so, it's probably
OK to just say that you are using it, and not bother writing its
proof. But if you have no idea at all how to prove it, then it may
well in fact not be true, and you should be wary! (If you can't see
any way of doing without the `fact', you can start off by saying
"Assuming it is true that..."; that way,your proof will still be true,
even if the hypothesis you need isn't!)
Homework 1, due Tuesday 22nd Jan
Read through section 1 of the
"knotes" and do exercises 1.2.6, 1.2.9, 1.2.10, 1.4.3, 1.6.2, 1.6.3,
1.6.7, 1.7.1, 1.7.2. (This first homework consists almost
entirely of "problems to make you think", rather than "this will be on
the exam"-type problems, so don't panic, treat it as an exercise in
playing around as an important part of mathematical research!)
Homework 2, due Monday Jan 29
Homework 3, due Monday Feb 4
2.3.10, 3.1.5, 3.1.6, 3.1.7, 3.1.8, 3.1.9, 3.1.10, 3.2.8, 3.2.12, 3.3.21Homework 4, due Monday Feb 11
3.3.22, 3.3.23, 3.3.24, 3.4.7, 3.4.8, 3.4.10, 4.1.7, 4.1.8, 4.1.9Homework 5
4.1.10, 4.1.11, 4.1.12, 4.4.5, 4.4.6, 4.5.4, 4.5.5, 4.5.6Homework 6
4.5.3, 4.5.7, 4.6.5, 4.6.7, 4.7.1; then read section 4.9 and do 4.9.4, 4.9.5, 4.9.6, 4.9.9 (the techniques are no different from the ones used with the Jones polynomial).Homework 7
6.1.2, 6.1.3, 6.2.7, 6.2.8, 6.2.12, 6.2.13, 6.2.14, 6.2.15. If you are careful about the first few, you should find it easier to be less careful about the later ones, which are more meant to get you used to some interesting behaviour of surfaces than as technical exercises!