Suppose `T_1` is a Young diagram of shape `\lambda=(\lambda_1,\lambda_2,\cdots,\lambda_k)` and `T_2` is a Young diagram of shape `\mu=(\mu_1,\mu_2,\cdots,\mu_j)`, where `\mu_i\leq \lambda_i`. If we subtract `T_2` from `T_1`, we get a skew Young diagram of shape `\lambda//\mu`.
For example, `S_1` is a skew Young tableau of shape `(5^2,3,2^2)//(2^2,1)` and `S_2` is a skew Young diagram of shape `(5,4,2^2,1)//(3,1)`.
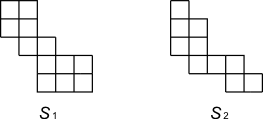
Suppose `\lambda` is a partition of `m+n` and `\mu` is a partition of `m`, a skew standard Young tableau of shape `\lambda // \mu` is obtained by filling `\{1,2,\cdots,n\}` in `n` boxes such that each column is increasing from bottom to top and each row is increasing from left to right. Unfornately, hook-length formula cannot be used for skew Young tableaux.
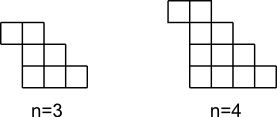
`a(n)` is the number of skew standard Young tableaux of shape `(n+1,n,n-1,\cdots,3,2) // (1^{n-1})`.
For example, skew diagrams of shape `(4,3,2) // (1^2)` and of shape `(5,4,3,2) // (1^3)` are as follows,
Find `a(n)`.