This exercise is about the number of linear partitions of `2`-by-`n` grid points.
We consider a set of lattice points, `\{1,2,\cdots,n\}\times\{1,2\}`. For example, the set of `2`-by-`4` gird points are pictured as follows.
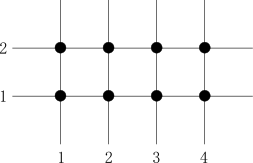
We want to partition these `2n` points into two nonempty parts by a straight line. An example of two different linear partitions of `2`-by-`4` grid points is pictured as follows.


Note that the area/size of grid points are not taken into consideration.
Suppose `a(n)` is the number of linear partitions of such `2\times n` grid points.
For example, `a(1)=1` and `a(2)=6`.
Find `a(n)`.