Suppose $F$ is an $n\times 2$ array with fillings of $\{1,2,3,\cdots,2n\}$ such that elements are increasing from bottom to top in each column. Clearly, there are $\binom{2n}{n}$ such arrays. We let $F(i,j)$ denote the element in the $i$-th row and $j$-th column, counting from bottom to top and left to right. If $F(i+1,1)-F(i,1)=1$ or $F(i+1,2)-F(i,2)=1$ for any $1\leq i \leq n-1$, we say $F$ is a degenerate array. This type of arrays were introduced by Harmse and Remmel in this paper.
For example, there are ten $3\times 2$ degenerate arrays, pictured as follows.
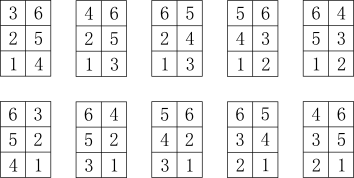
Suppose we let $a_n$ denote the number of $n\times 2$ degenerate array.
Find $a_n$.