


Next: About this document
Math15A - Discrete Mathematics
Suggestions on How to Write Proofs
Sam Buss - April 1999
One way to define mathematics is that is the study of structures
which can be precisely and unambiguously defined. These structures
include things like the integers, real numbers, geometrical objects,
functions, relations, etc. Since these objects can be unambiguously
defined, it is possible to establish truths about these objects
which are known to be true beyond any reasonable doubt. Mathematical
proofs are used to establish these kinds of mathematical truths:
the purpose of proof is convince both its author and its readers that
certain theorems are true.
In Math 15A, we will teach (mainly by example) various approaches to
writing proofs: these approaches tend to be oriented towards how
to use common proof strategies, and how to obey the generally accepted
conventions of writing proofs.
Reading proofs: Before one can write proofs, one needs to be
able to read proofs. Here the general guidelines are:
- Read the proof sceptically. An effective
proof should drag you to a conclusion
even if you are disinclined to accept the conclusion. Try
not to let the proof's author fool you by skipping any steps:
if steps are skipped, then you have to fill them in yourself.
If the author uses any unproved assumptions, then you should notice this.
The bumper sticker ``Question Authority'' definitely applies to
the authors and readers of mathematical proofs: you should expect
a proof to convince you, and to not need to take assertions
on faith or authority.
- Before you start reading the proof, think about what needs to
be proved and how one would naturally go about trying to prove it.
This will help you understand why certain steps are taken
(and may help you fill in the steps skipped by the author).
- Read every word of the proof, and understand every assertion
made in the proof. Proofs are generally tersely worded and one cannot
understand a proof if a single line is misunderstood.
- You have the right to demand of the proof author that the
proof be written correctly, using correct grammar, complete sentence,
and correct mathematical syntax.
Some general guidelines for writing proofs are:
-
Before you try to write a proof, express the theorem in (semi-)formal
language, including all the quantifiers, etc., in proper syntax.
-
Start the proof with the word ``Proof''.
End the proof with ``Q.E.D.'', Latin for ``it is demonstrated''.
-
Write your proof in correct grammar: use complete sentences, follow
correct English grammar, use conventional and syntactically correct
mathematical expressions.
-
State your assumptions clearly.
-
Explain every step that is taken in the proof. For instance, if you
are about to embark on a proof by contradiction, say that the
proof is by contradiction and state precisely the assumption that
is being made (that will disproved by deriving a contradiction).
Likewise, a proof by induction should clearly and precisely
state the statement being
proved by induction.
-
Keep your audience in mind and write the proof at level
appropriate for your readers. In a course like Math 15A, the
proofs should be written more-or-less in the style used in the
text or presented in class. However, both the text and the instructor
may get sloppy at times and present less detail than they really
should (the instructor can get away with this partly since he can explain
things verbally too, and partly since students are sometimes reluctant
to ask questions). Your proofs may need to use a little more detail than
the text and the instructor.
-
Don't use the same variable for two different purposes.
-
Avoid logical fallacies!
Finding proofs can be a tremendously hard process and require
a lot of both creativity and luck. Even after the creative insight,
it may take a lot of work to structure the proof clearly and actually
write out the proof.
In Math 15A, you will be asked to prove only relatively straightforward
theorems. The following guidelines should be helpful for finding
proofs:



Next: About this document
Sam Buss
Mon Apr 26 22:00:37 PDT 1999
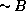 is true and prove
is true and prove 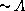 . (I.e, prove the
contrapositive of
. (I.e, prove the
contrapositive of 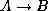 .)
.)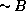 are true and derive a contradiction.
are true and derive a contradiction.