Research
My research interests include numerical linear algebra, geometric numerical integration, and numerical stochastic methods. My adviser is Melvin Leok. My thesis research focuses on a class of symplectic integrators, known as variational integrators. These numerical methods preserve qualitative features of a dynamical system, which often are defined by the geometry and topology of the system. For instance, a variational integrator transforms a continuous Hamiltonian system into a discrete Hamiltonian system, which preserves the symplectic geometry and can be viewed as a perturbed version of the original system. As a result the integrator exhibits long-time near-energy preservation as well as discrete Noether quantities. For further information, please see my CV. My thesis can be found here.Research projects
| ◉ | Taylor Variational Integrators with T. Shingel, M. Leok submitted to BIT Numerical Mathematics [article] | |
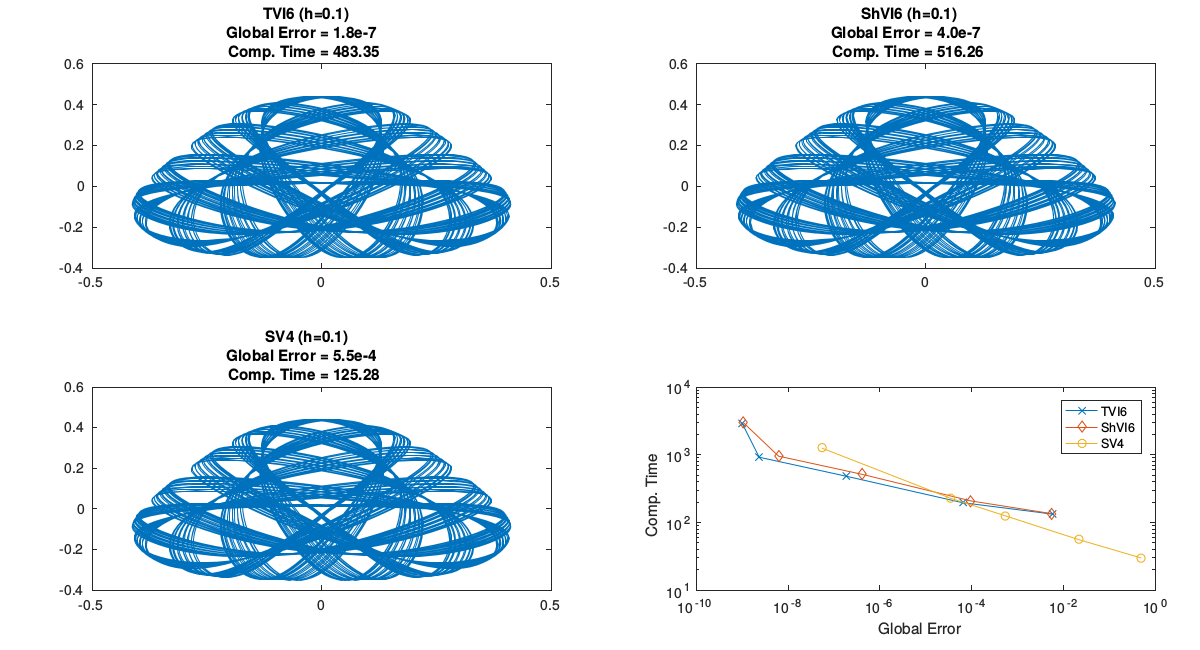 | In this paper, we present a variational integrator that is based on an approximation of the Euler--Lagrange boundary-value problem via Taylor's method. This method is more efficient than using other one-step methods, since Taylor's method can be used to compute the discrete solution at the quadrature nodes at the cost of a polynomial evaluation once the prolongation of the Euler--Lagrange vector field is computed at the initial time. In addition, the resulting symplectic and variational integrator is one order higher than the order of the underlying Taylor's method. | |
| ◉ | Properties of Hamiltonian Variational Integrators with M. Leok published in IMA Journal of Numerical Analysis [article] | |
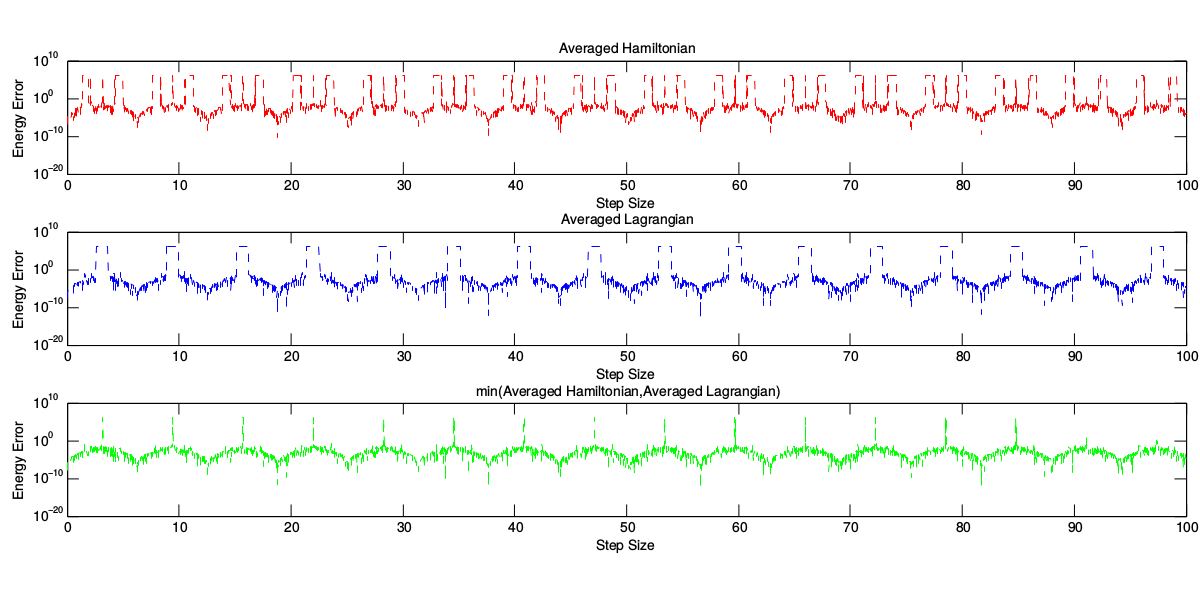 | Discrete Hamiltonian variational integrators are derived from Type II and Type III generating functions for symplectic maps, and in this paper we establish a variational error analysis result that relates the order of accuracy of the associated numerical methods with the extent to which these generating functions approximate the exact discrete Hamiltonians. We also introduce the notion of an adjoint discrete Hamiltonian, and relate it to the adjoint of the associated symplectic integrator. We show that when constructing discrete Lagrangians and discrete Hamiltonians using the same approximation method this does not necessarily lead to the same symplectic integrator. Numerical experiments also indicate that the resonance behavior of variational integrators based on averaging methods, depends on the type of generating functions used, and we relate this resonance behavior to the ill-posedness of the boundary-value problems used to define the exact discrete Lagrangian and exact discrete Hamiltonian. | |
| ◉ | Adaptive Variational Integrators with M. Leok in preperation | |
| ◉ | Stochastic Variational Integrators
[article] | |
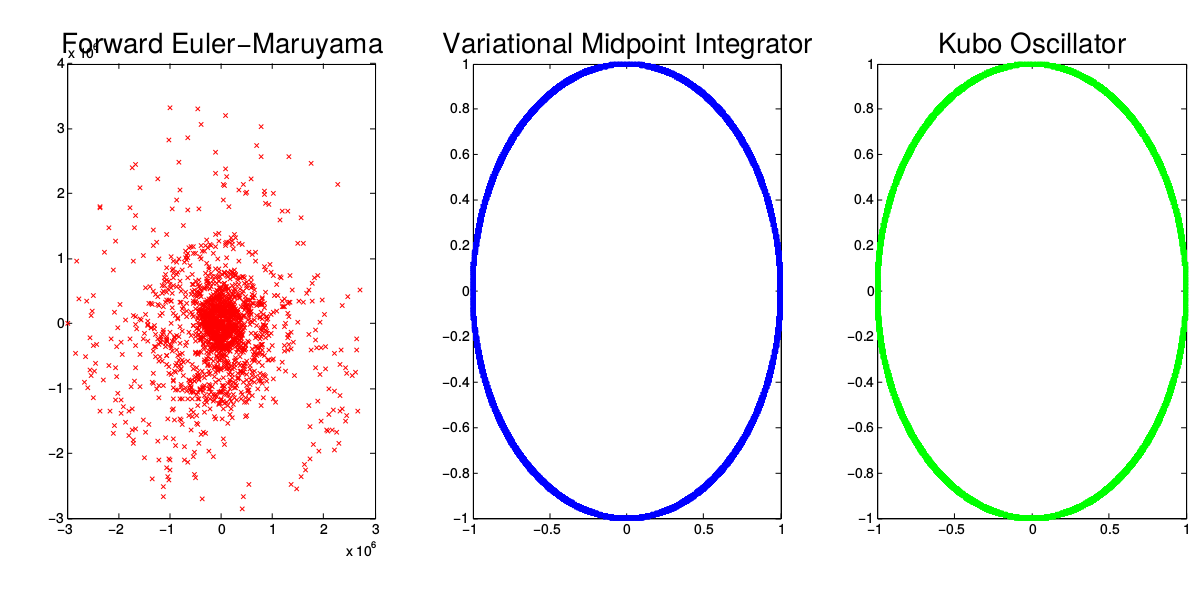 | Variational integrators are numerical geometric integrator's derived from discretizing Hamilton's principle. They are symplectic integrators that exhibit excellent long-term stability, near-energy preservation and preserve many invariants of the underlying dynamical system. In particular, it has been shown that variational integrators perform very well when computing statistics of the system such as Poincare sections or instantaneous temperature. These reasons and more spurred the extension of variational integrators to stochastic differential equations. Symplectic integrators have already played an important role in stochastic simulations via the Hybrid/Hamiltonian Monte Carlo method, but have only recently been extended as direct stochastic integrators. In this paper we examine the performance of stochastic variational integrators through numerical experimentation, and compare them with standard methods for stochastic differential equations. | |