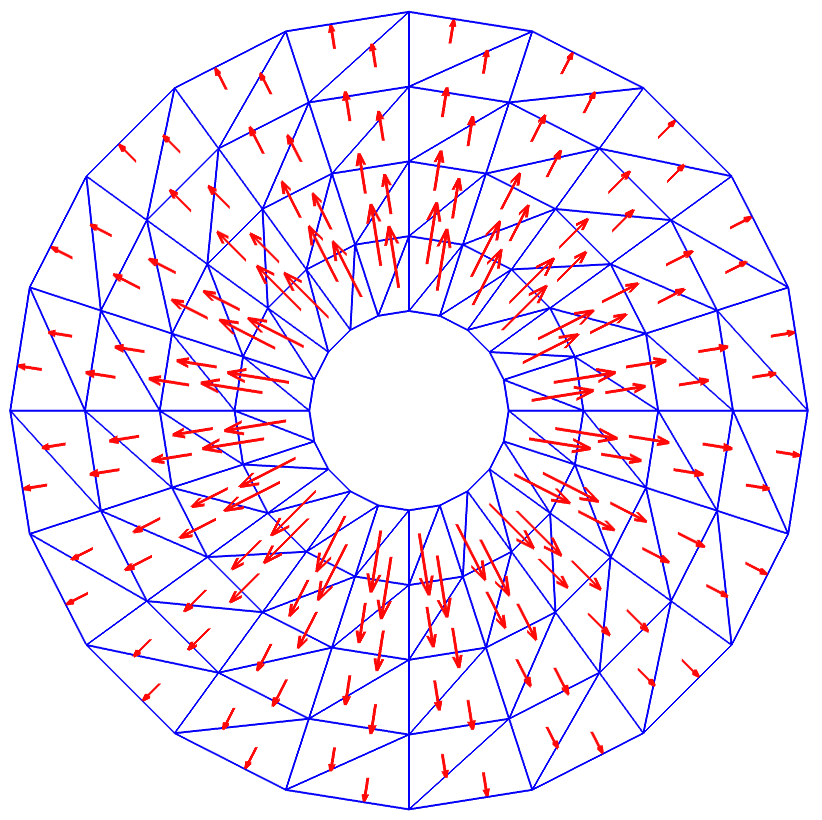
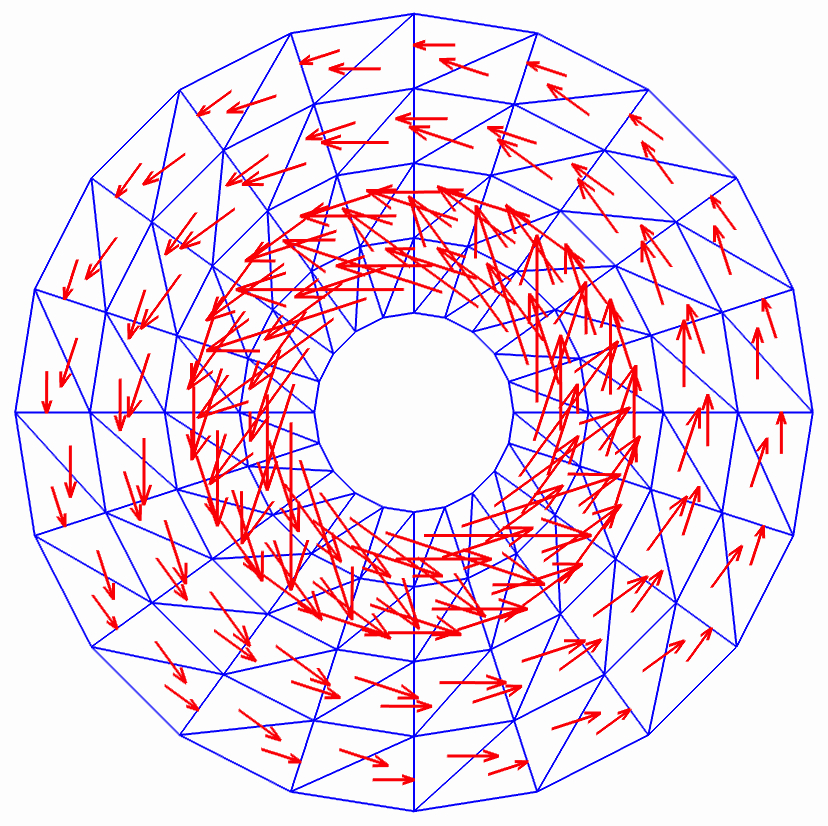
Research Interests

My research develops around structure-preserving numerical methods for partial differential equations. This has been a very active area of research in the past years. The basic »paradigm« of structure-preserving numerical methods is to mimic qualitative properties of the analytical problem on a discrete level, since qualitative properties, such as energy conservation, are often very important for practical applications in physics and industry. The mathematical beauty of these methods lies in the confluence of numerical, global, and functional analysis, of differential geometry and algebraic topology.

I focus on finite element exterior calculus, whose main idea is to construct a de Rham complex of spaces of finite element differential forms. Not only does it provide a very powerful tool in the construction and understanding of finite element methods, but gives the background for a productive exchange in pure and applied analysis. In fact, one can discover that many similar ideas have been used in finite element analysis and global analysis.

The theory of these methods is mathematically very demanding (which might explain my passion for this research area). I am convinced this mathematics is necessary for effectively mastering complex problems in computational physics. I value thorough and detailed research, and it is my ambition to keep the big picture in perspective; in fact, keeping an eye on the details is often necessary to fully comprehend mathematics in the big picture, and to discover often surprising new insights.